算法笔记：并查集（union-find算法）

问题建模

动态连通性问题

对于一类问题，问题的输入是一些对象两两之间的“相连关系”，并且这种“相连关系”是一种等价关系，即它具有以下性质：

自反性：任何对象和其自身都是相连的；
对称性：如果p和q是相连的，那么q和p也是相连的；
传递性：如果p和q是相连的，q和r是相连的，那么p和r也是相连的。

那么我们可以把相连的对象划分为一个等价类。问题的目标是根据输入的所有相连关系，将对象空间划分为多个等价类，并能够判断任意两个对象是否属于同一个等价类。这个问题称为动态连通性问题，动态连通性问题有以下现实场景的应用：

网络：输入的对象表示一个大型计算机网络中的计算机，相连关系表示计算机之间的连接，那么只有属于同一个等价类的两台计算机才能相互通信；或者也可以是社交网络，即对象是人，相连关系表示人之间的朋友关系，那么可以将人划分为“朋友圈”(即等价类)。
数学集合：抽象地说，可以将相连关系看作“属于同一个集合”。

将问题抽象完成后，引入一些术语：将对象称为触点，将相连关系称为连接，将等价类称为连通分量或者简称分量。为了描述方便，直接 $0$ 到 $N-1$ 的整数表示 $N$ 个触点。

算法API

将动态连通性问题的解决抽象为一份API：

public class UF {
    // 以整数标识（0到N-1）初始化N个触点
    UF(int N);

    // 在p和q之间添加连接
    void union(int p, int q);

    // p所在的分量（分量也由整数表示），要保证当参数属于同一个分量时，返回值应该相等。
    int find(int p);

    // 判断p和q是否在同一个分量中
    boolean connected(int p, int q);

    // 连通分量的数量
    int count();

}

实现时要注意以下要点：

所有的对象是用0到N-1表示的
连通分量也用整数表示，一般来说可以用该分量中任意一个对象来表示。

为了实现上述功能，我们用一个整数数组id[]来记录所有的对象所属的分量。即id[p]表示的是对象p所属的连通分量。那么有以下实现

public class UF {
    private int[] id;
    // 记录分量的个数
    private count;

    public UF(int n) {
        // 初始化时，所有触点都是一个独立的分量
        count = n;
        id = new int[n];
        // 所有触点都构成了一个只含有它自己的分量，因此将id[i]的值初始化为i
        for(int i = 0; i < n; i++) {
            id[i] = i;
        }
    }

    public int count() { return count; }

    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
}

其中find()和union()两个方法有不同的实现。

实现

quick-find算法

这种方法是要保证当且仅当id[p]等于id[p]时，p和q是属于同一个分量的。此时实现如下

public int find(int p) {
    return id[p];
}

public void union(int p, int q) {
    int pId = find(p);
    int qId = find(q);

    // 只有在p和q不属于同一个分量时才需要执行
    if(pId != qId) {
        // 将所有与p同一分量的触点所属的分量修改为q所属的分量
        for(int i = 0; i < id.length; i++) {
            if(id[i] == pId) {
                id[i] = qId;
            }
        }
        count--;
    }
}

分析：

find()操作的时间复杂度为 $O(1)$ ，因为只需要访问一次id数组
union()操作的时间复杂度为 $O(N)$ ，因为每一个合并都需要遍历整个id数组
如果有M对连接，那么构建出所有的分量的时间复杂度为 $O(MN)$ 。

quick-union算法

这种方法不需要保证同一个分量中的触点的id值相同，id[]值只是同一个分量中另一个触点（或者也可以是触点自身），此时每一个分量中必定有一个触点的id值是指向自身的，这个触点就可以被认为是该分量的“根触点”，用以代表整个分量。

public int find(int p, int q) {
    while(p != id[p]) p = id[p];
    return p;
}

public void union(int p, int q) {
    // 将p和q的根触点统一
    int pRoot = find(p);
    int qRoot = find(q);

    if(pRoot != qRoot) {
        id[pRoot] = qRoot;
        count --;
    }
}

这种方法其实是用一棵树来表示一个分量，整个id数组用父连接的形式表现了一片森林。

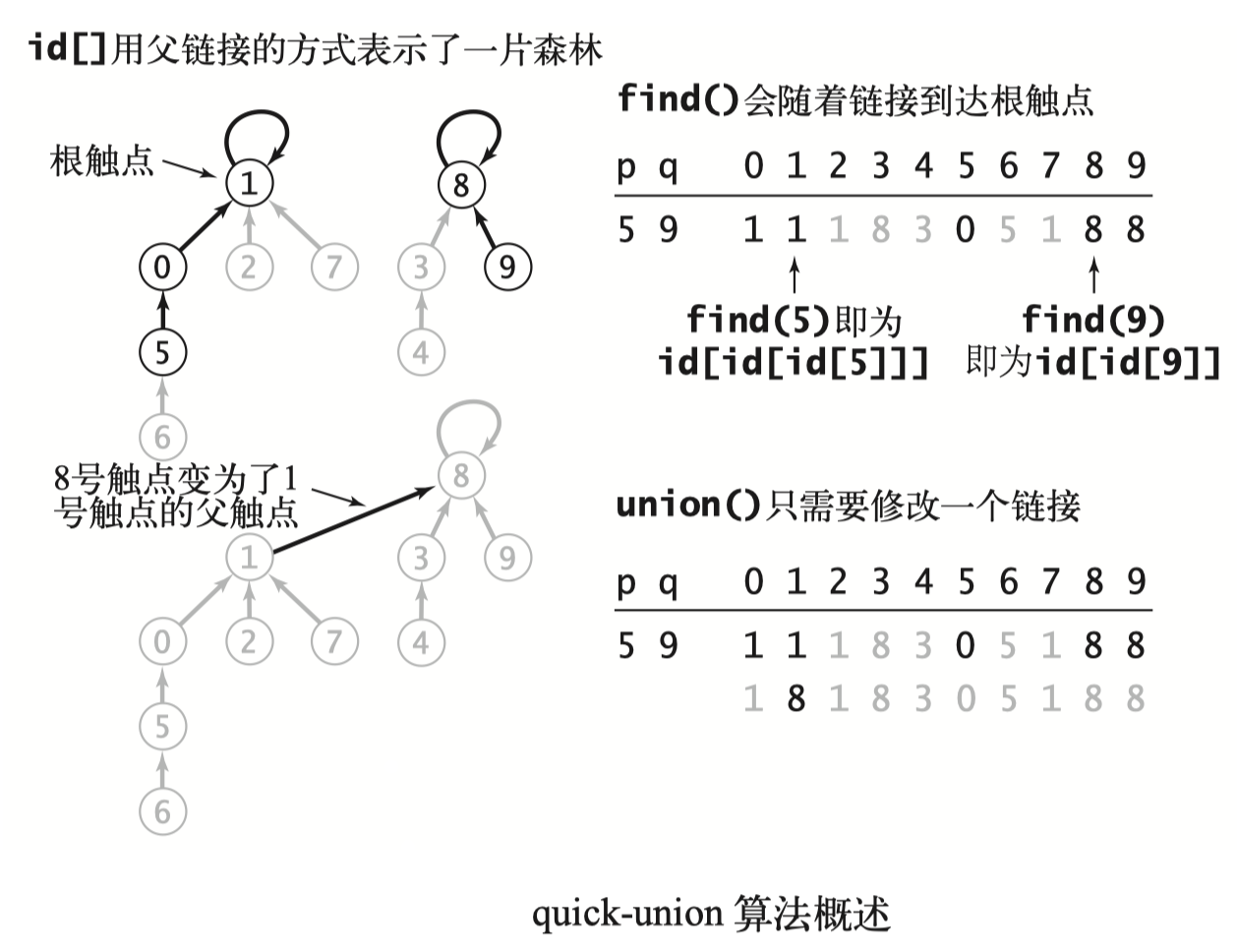
分析：

最好情况下，find()操作的时间复杂度是 $O(1)$ ，最坏情况下，find()操作的时间复杂度是 $O(N)$
union()操作的时间复杂度应该与find()操作是一致的。

加权quick-union算法

为了防止最坏情况的出现，需要对quick-union算法进行优化，在quick-union算法中，union()操作是随意的将一棵树连接到另一棵树，改进的方法就是记录每一棵树的大小并总是将较小的树连接到较大的树上。这种方法称为加权quick-union算法。这项改动需要添加一个数组和一些代码来记录树中的节点树。实现如下：

public class WeightedQuickUnionUF {
    private int[] id;
    private int[] size;
    private int count;

    public WeightedQuickUnionUF(int n) {
        count = n;
        id = new int[n];
        for(int i = 0; i < n; i++) id[i] = i;
        size = new int[n];
        for(int i = 0; i < n; i++) size[i] = 1;
    }

    public int count() { return count; }

    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    public int find(int p) {
        while(p != id[p]) p = id[p];
        return p;
    }

    public void union(int p, int q) {
        int i = find(p);
        int j = find(q);
        if(i == j) return;
        if(size[i] < size[j]) {
            id[i] = j;
            size[j] += size[i];
        } else {
            id[j] = i;
            size[i] += size[j];
        }
        count--;
    }
 }

分析：

对于 $N$ 个触点，该算法构造的森林中任意的节点的深度最多为 $\log{N}$
find()操作的时间复杂度为 $O(\log{N})$ ，union()操作的时间复杂度为 $O(\log{N})$
对于 $N$ 个触点， $M$ 对连接，那么构建出所有的分量的时间复杂度为 $O(M\log{N})$
路径压缩：如果需要进一步优化，可以在检查节点的同时将它直接连接到根节点。该过程称为路径压缩

例题

(LeetCode. 547)班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。
给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例1:

输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

示例2:

输入:
[[1,1,0],
[1,1,1],
[0,1,1]]
输出: 1
说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。

注意：

N 在[1,200]的范围内。

对于所有学生，有M[i][i] = 1。

如果有M[i][j] = 1，则有M[j][i] = 1。

题解：

class Solution {
    public int findCircleNum(int[][] M) {
        int n = M.length;
        UF uf = new UF(n);
        for (int i = 0; i < n; i++) {
            for (int j = i+1; j < n; j++) {
                if(M[i][j] == 1) {
                    uf.union(i, j);
                }
            }
        }
        return uf.count();
    }
    class UF {
        int[] id;
        int[] size;
        int count;
        public UF(int n) {
            id = new int[n];
            for (int i = 0; i < n; i++) id[i] = i;
            size = new int[n];
            for (int i = 0; i < n; i++) size[i] = 1;
            count = n;
        }
        public int count() { return count;}

        public int find(int p) {
            while (p != id[p]) p = id[p];
            return p;
        }

        public void union(int p, int q) {
            int pRoot = find(p);
            int qRoot = find(q);
            if(pRoot == qRoot) return;
            if(size[pRoot] < size[qRoot]) {
                id[pRoot] = qRoot;
                size[qRoot] += size[pRoot];
            } else {
                id[qRoot] = pRoot;
                size[pRoot] += size[qRoot];
            }
            count--;
        }
    }
}